The poly-hyperbolic function \(h_{kl}(z)\) is defined as the infinite series
\begin{equation*}
h_{kl}(z) \equiv \sum_{n = 0}^{\infty} \frac{1}{\Gamma(kn + l + 1)} z^{kn + l}
\end{equation*}
Here \(k \geq 1\) and \(0 \leq l \leq k - 1\). The integer \(k\) is called the grade. For a fixed even value of \(k\), the resulting \(k\) functions behave like hyperbolic functions.
Note that
\begin{equation*}
\exp{(z)} = \sum_{l = 0}^{k-1} h_{kl}(z)
\end{equation*}
You can also define two kinds of ratios:
\begin{align*}
S_{kmn}(z) &= \frac{h_{km}(z)}{h_{kn}(z)} & U_{kmn}(z) &= \frac{h_{km}(z)}{h_{kn}(z)}
\end{align*}
For both \(S_{kmn}\) and \(U_{kmn}\) you have \(m > n\) but \(m\) and \(n\) are either both even or both odd for \(U_{kmn}\). Either \(m\) is even and \(n\) is odd, or vice-versa, for \(S_{kmn}\).
Let us look at three specific cases.
2-Graded
You have two functions:
\begin{align*}
h_{20}(z) &= \cosh{(z)} & h_{21}(z) &= \sinh{(z)}
\end{align*}
Note the differentiation identities:
\begin{align*}
\frac{d h_{21}}{dz} &= h_{20} & \frac{d h_{20}}{dz} &= h_{21}
\end{align*}
The only possible ratio is
\begin{equation*}
S_{210}(z) = \frac{h_{21}(z)}{h_{20}(z)} = \tanh{(z)}
\end{equation*}
This ratio behaves like a monotonic sigmoid.
4-Graded
You have four functions:
\begin{align*}
h_{40}(z) &= \frac{\cosh{(z)} + \cos{(z)}}{2} & h_{41}(z) &= \frac{\sinh{(z)} + \sin{(z)}}{2} \\
h_{42}(z) &= \frac{\cosh{(z)} - \cos{(z)}}{2} & h_{43}(z) &= \frac{\sinh{(z)} - \sin{(z)}}{2}
\end{align*}
Note the differentiation identities:
\begin{align*}
\frac{d h_{43}}{dz} &= h_{42} & \frac{d h_{42}}{dz} &= h_{41} & \frac{d h_{41}}{dz} &= h_{40} & \frac{d h_{40}}{dz} &= h_{43}
\end{align*}
There are six possible ratios. Four of them are of the \(S\)-kind:
\begin{align*}
S_{410}(z) &= \frac{h_{41}(z)}{h_{40}(z)} & S_{421}(z) &= \frac{h_{42}(z)}{h_{41}(z)} \\
S_{430}(z) &= \frac{h_{43}(z)}{h_{40}(z)} & S_{432}(z) &= \frac{h_{43}(z)}{h_{42}(z)}
\end{align*}
Here is a graph of \(S_{410}(z)\): 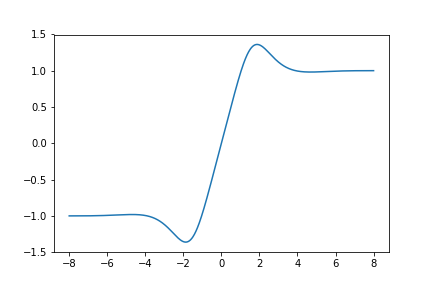
Here is a graph of the derivative of \(S_{410}(z)\): 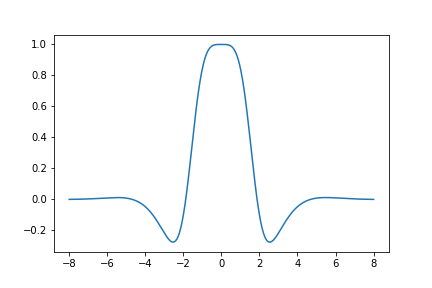
Here is a graph of \(S_{421}(z)\): 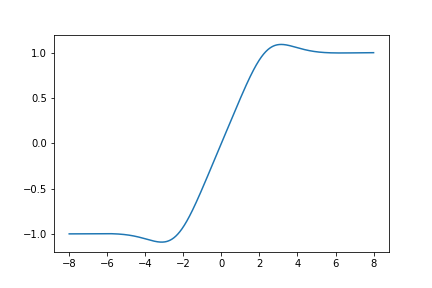
Here is a graph of the derivative of \(S_{421}(z)\): 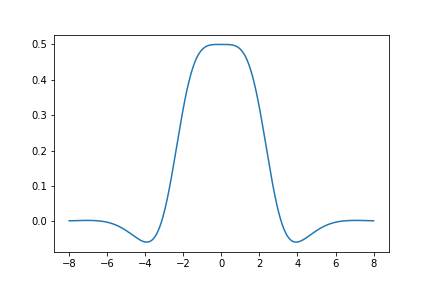
Here is a graph of \(S_{430}(z)\): 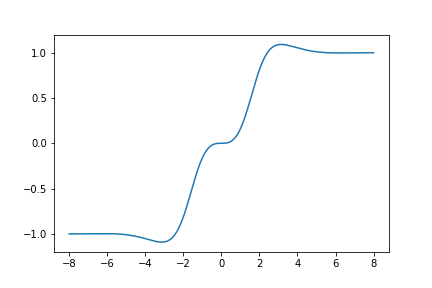
Here is a graph of the derivative of \(S_{430}(z)\): 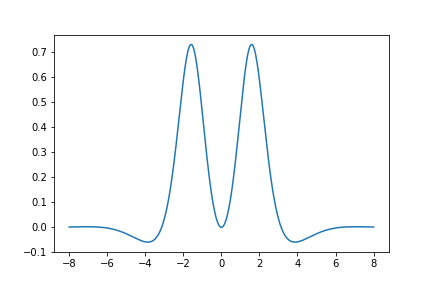
Here is a graph of \(S_{432}(z)\): 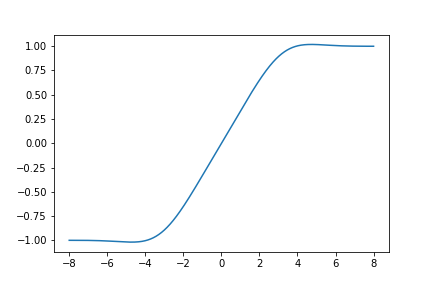
Here is a graph of the derivative of \(S_{432}(z)\): 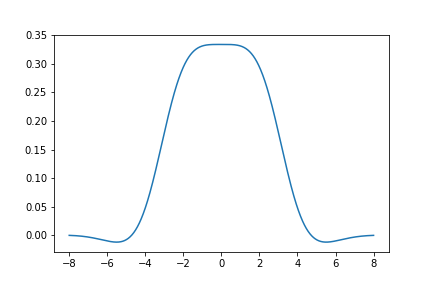
The other two are of the \(U\)-kind:
\begin{align*}
U_{420}(z) &= \frac{h_{42}(z)}{h_{40}(z)} & U_{431}(z) &= \frac{h_{43}(z)}{h_{41}(z)}
\end{align*}
Here is a graph of \(U_{420}(z)\): 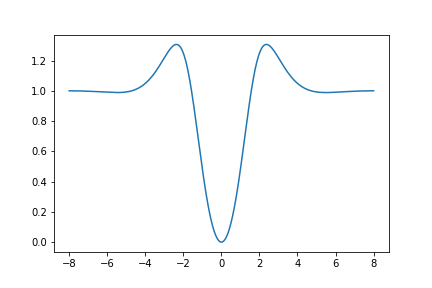
Here is a graph of the derivative of \(U_{420}(z)\): 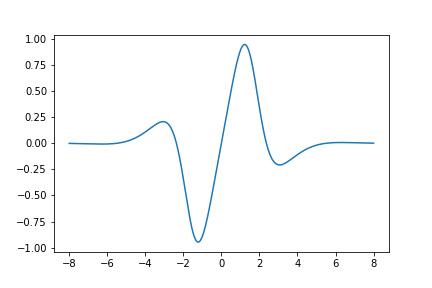
Here is a graph of \(U_{431}(z)\): 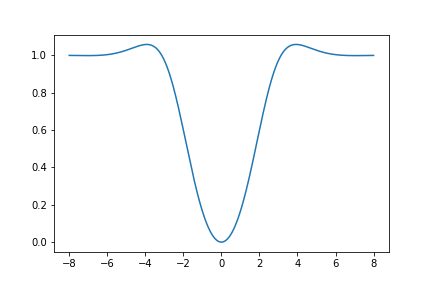
Here is a graph of the derivative of \(U_{431}(z)\): 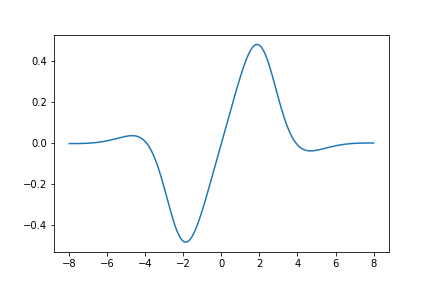
Note that
\begin{align*}
\frac{d S_{410}}{dz} &= 1 - S_{410} S_{430} & \frac{d S_{421}}{dz} &= 1 - \frac{S_{421}}{S_{410}} \\
\frac{d S_{430}}{dz} &= U_{420} - S_{430}^{2} & \frac{d S_{432}}{dz} &= 1 - \frac{S_{432}}{S_{421}} \\
\frac{d U_{420}}{dz} &= S_{410} - U_{420} S_{430} & \frac{d U_{431}}{dz} &= S_{421} - \frac{U_{431}}{S_{410}}
\end{align*}
These relations generalize the derivatives of the hyperbolic tangent.
6-Graded
There are six functions. You have the differentiation identities:
\begin{align*}
\frac{d h_{65}}{dz} &= h_{64} & \frac{d h_{64}}{dz} &= h_{63} & \frac{d h_{63}}{dz} &= h_{62} & \frac{d h_{62}}{dz} &= h_{61} & \frac{d h_{61}}{dz} &= h_{60} & \frac{d h_{60}}{dz} &= h_{65}
\end{align*}
With these six functions you can construct 15 ratios. Of these, 9 ratios are of \(S\)-kind:
\begin{align*}
S_{610}(z) &= \frac{h_{61}(z)}{h_{60}(z)} & S_{621}(z) &= \frac{h_{62}(z)}{h_{61}(z)} & S_{630}(z) &= \frac{h_{63}(z)}{h_{60}(z)} \\
S_{632}(z) &= \frac{h_{63}(z)}{h_{62}(z)} & S_{643}(z) &= \frac{h_{64}(z)}{h_{63}(z)} & S_{641}(z) &= \frac{h_{64}(z)}{h_{61}(z)} \\
S_{654}(z) &= \frac{h_{65}(z)}{h_{64}(z)} & S_{652}(z) &= \frac{h_{65}(z)}{h_{62}(z)} & S_{650}(z) &= \frac{h_{65}(z)}{h_{60}(z)}
\end{align*}
Here is a graph of \(S_{610}(z)\): 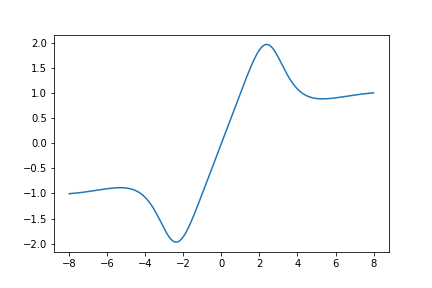
Here is a graph of \(S_{621}(z)\): 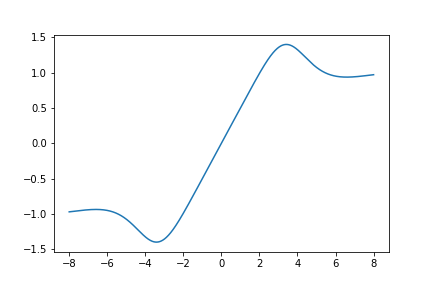
Here is a graph of \(S_{630}(z)\): 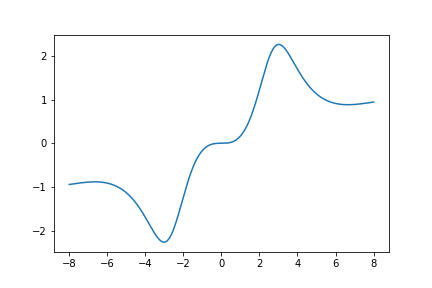
Here is a graph of \(S_{632}(z)\): 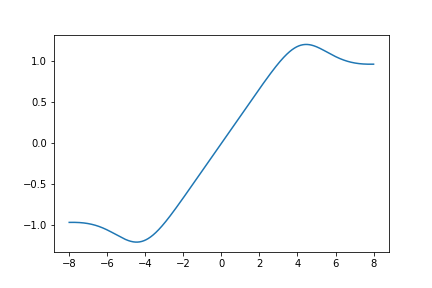
Here is a graph of \(S_{641}(z)\): 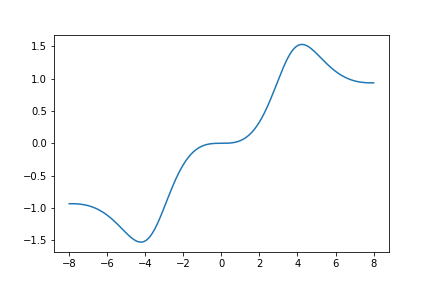
Here is a graph of \(S_{643}(z)\): 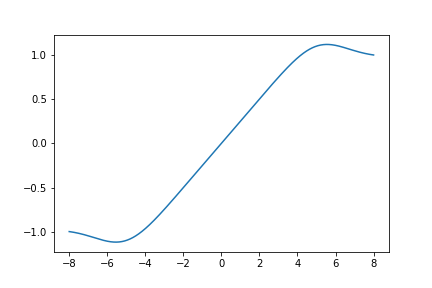
Here is a graph of \(S_{650}(z)\): 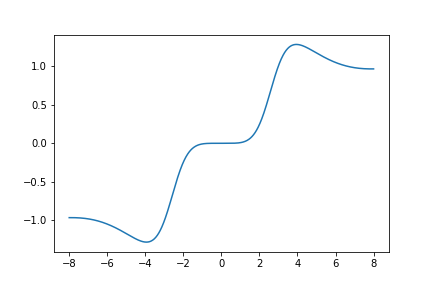
Here is a graph of \(S_{652}(z)\): 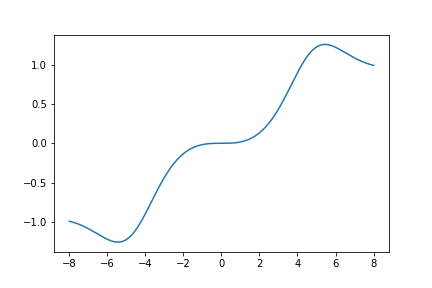
Here is a graph of \(S_{654}(z)\): 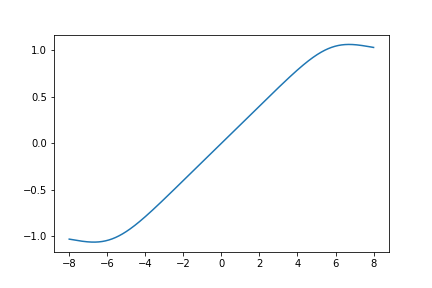
The other 6 ratios are of \(U\)-kind:
\begin{align*}
U_{620}(z) &= \frac{h_{62}(z)}{h_{60}(z)} & U_{631}(z) &= \frac{h_{63}(z)}{h_{61}(z)} & U_{642}(z) &= \frac{h_{64}(z)}{h_{62}(z)} \\
U_{640}(z) &= \frac{h_{64}(z)}{h_{60}(z)} & U_{653}(z) &= \frac{h_{65}(z)}{h_{63}(z)} & U_{651}(z) &= \frac{h_{65}(z)}{h_{61}(z)}
\end{align*}
Here is a graph of \(U_{620}(z)\): 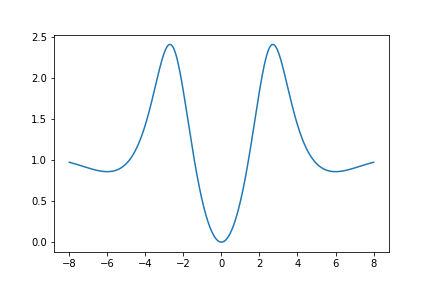
Here is a graph of \(U_{631}(z)\): 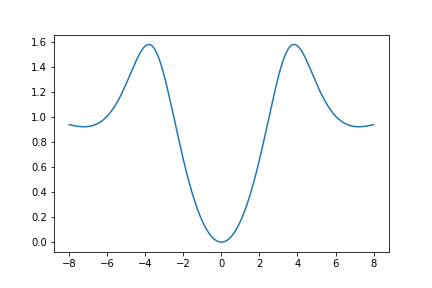
Here is a graph of \(U_{640}(z)\): 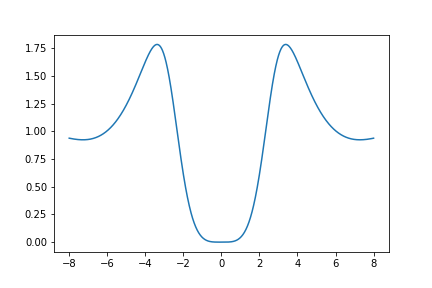
Here is a graph of \(U_{642}(z)\): 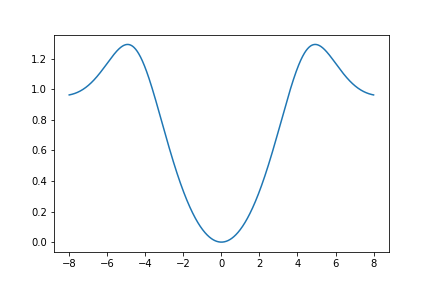
Here is a graph of \(U_{651}(z)\): 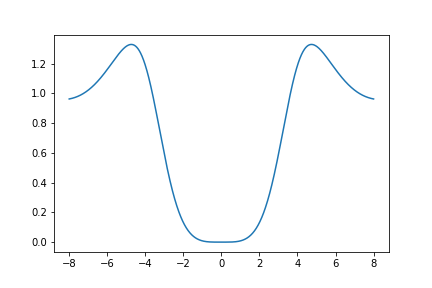
Here is a graph of \(U_{653}(z)\): 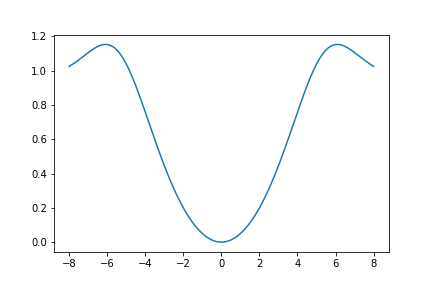
Applications in Neural Networks
The hyperbolic tangent is used in neural networks as an activation function. Although the functions described here are not monotonic, they might still be useful.



























